Maximum Depth of Binary Tree (Leetcode #104)
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:
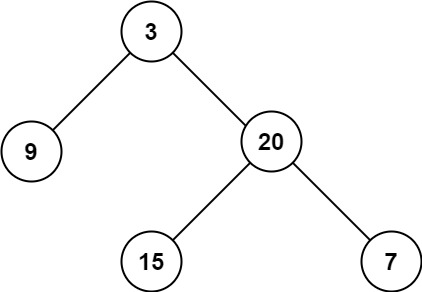
Input: root = [3,9,20,null,null,15,7]
Output: 3
Example 2:
Input: root = [1,null,2]
Output: 2
Constraints:
The number of nodes in the tree is in the range
[0, 10<sup>4</sup>].-100 <= Node.val <= 100
Answer
In this question, we use the Depth-First Search (DFS) algorithm. The maximum depth of each node is calculated as 1 plus the maximum depth of its children. This means we start from the bottom of the tree, determining the depth of each left and right subtree recursively, and then work our way up to the root. The depth of the root node ultimately gives us the maximum depth of the entire tree.
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root:
return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
Time Complexity
The time complexity is O(N) because we visit each node exactly once.
Space Complexity
The space complexity depends on the height of the tree. If the tree is balanced, the recursion depth is O(log N), resulting in a space complexity of O(log N). However, in the worst case, where the tree is completely unbalanced, the space complexity is O(N).