Balanced Binary Tree (Leetcode #110)

Given a binary tree, determine if it is height-balanced

.A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Example 1:

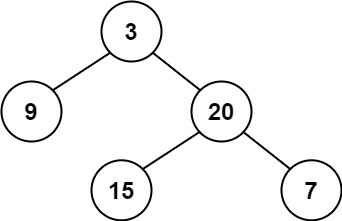
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

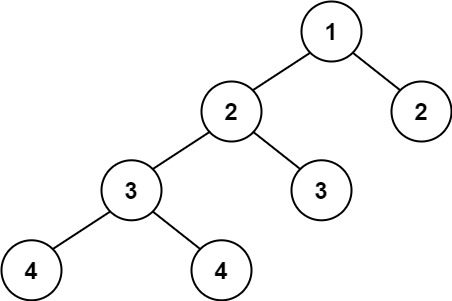
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].

• -10<sup>4</sup> <= Node.val <= 10<sup>4</sup>

Answer

To solve this problem we will use a similar method we use with the Diameter of Binary Tree question where we solve this from the bottom up.

1. If we treat each node as a tree then the tree can only be balanced if the left node is balanced, the right node is balanced and the height of the left and right node can not exceed one.

2. Looking at step one our output must include two things:

   1. If the current node is balanced

   2. the max height of the node

3. Knowing all these conditions we can solve the problem using DFS

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        def dfs(root):
            if not root:
                return [True,0]
            left = dfs(root.left)
            right = dfs(root.right)
            balance = (left[0] and right[0] and abs(left[1] - right[1]) <= 1) #Checked if the tree is balance
            return [balance, 1+max(left[1], right[1])]
        return dfs(root)[0]

Looking at the code you can see that we are outputting two things:

[If the current node balance, The max height of the node]

Time Complexity: O(N)

Space Complexity: O(logN) best case and O(N) worst case