Algo

Binary Tree Level Order Traversal (Leetcode #102)

Nawat Sunthornyanakit's photo
Nawat Sunthornyanakit
·

3 min read

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

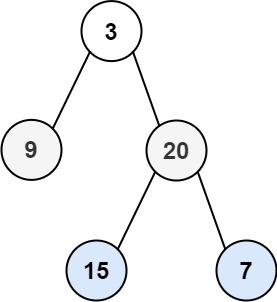
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 2000].

  • -1000 <= Node.val <= 1000

Answer

This is a great question since it introduced us to a new algorithm BFS (Breadth-First Search). Unlike DFS this method go though the binary tree level by level until we reach the lowest layer.

BFS

Breadth-First Search (BFS) is an algorithm used to traverse or search through a graph or tree data structure. It explores nodes level by level, starting from the root (or starting node) and expanding outwards. Here's a brief explanation:

Key Concepts:

  1. Level-by-Level Exploration: BFS visits all nodes at the present depth level before moving on to nodes at the next depth level.

  2. Queue-Based: BFS uses a queue to keep track of nodes to be explored. Nodes are added to the queue when they are first discovered and removed when they are explored.

  3. Algorithm Steps:

    • Initialize a queue with the starting node.

    • While the queue is not empty:

      • Dequeue a node.

      • Process the node (e.g., print its value, check if it's the target).

      • Enqueue all unvisited neighboring nodes of the current node.

Example:

For a tree:

mathematicaCopy code       A
      / \
     B   C
    / \
   D   E

BFS traversal starting from node A would visit nodes in the order: A, B, C, D, E.

Applications:

  • Finding the shortest path in an unweighted graph.

  • Level-order traversal of a tree.

  • Network broadcasting.

BFS is useful for problems where the shortest path or the level-order exploration is needed.

Applying this method to this question we will get something like

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        q = collections.deque()
        q.append(root)
        while q:
            temp = []
            for i in range(len(q)):
                node = q.popleft()
                if node:
                    temp.append(node.val)
                    q.append(node.left)
                    q.append(node.right)
            if temp:
                res.append(temp)
        return res

Time complexity is O(N) since we have to go through each node ounce and since is a deque the popleft is O(1) hence O(N) * O(1) = O(N)

Space Complexity is O(N) since we are storing each node as an output and each node are store for the next loop

leetcodePython