Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

Return the number of good nodes in the binary tree.

Example 1:

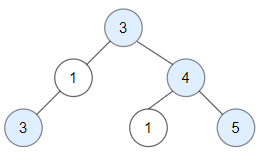
Input: root = [3,1,4,3,null,1,5]
Output: 4
Explanation: Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.

Example 2:

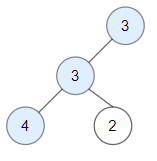
Input: root = [3,3,null,4,2]
Output: 3
Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.

Example 3:

Input: root = [1]
Output: 1
Explanation: Root is considered as good.

Constraints:

The number of nodes in the binary tree is in the range [1, 10^5].
Each node's value is between [-10^4, 10^4].

Answer

The problem asks us to find the number of nodes that are considered good. A good node is a node where, from the root to X, there are no nodes with a value greater than X. We will use a Depth-First Search (DFS) approach to solve this problem.

Approach:

Information Needed:
- The maximum value encountered so far in the path from the root to the current node.
- The current node's value.
Steps:
- If the current node is None, return 0 since there are no good nodes to consider.
- Compare the current node’s value with the maximum value along the path.
- If the current node's value is greater than or equal to the maximum, it is considered a good node:
  - Increase the count of good nodes.
  - Update the maximum value with the current node’s value.
- Recursively check the left and right children, passing the updated maximum value along the path.
- Sum up the results from the left and right subtrees.

Python Code:

pythonCopy code# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution(object):
    def goodNodes(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def dfs(root, max_val):
            if not root:
                return 0
            if root.val >= max_val:
                res = 1
                max_val = max(max_val, root.val)
            else:
                res = 0
            res += dfs(root.left, max_val)
            res += dfs(root.right, max_val)
            return res
        return dfs(root, -float('inf'))

Summary:

We use a DFS approach to determine if a node is good. If the node is good, we increase the count of good nodes and update the maximum value seen so far. The algorithm continues recursively to check all nodes and returns the total count of good nodes.

Time Complexity:

The time complexity is O(N) because we visit each node once. The comparison and updating operations are O(1), so the overall complexity is O(N).

Space Complexity:

The space complexity depends on whether the tree is balanced:
- In a balanced tree, the recursion stack's depth will be O(log N).
- In an unbalanced tree, the recursion stack could go up to O(N) in the worst case.

Count Good Nodes in Binary Tree (Leetcode #1448)

Answer