Diameter of Binary Tree (Leetcode #543)

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

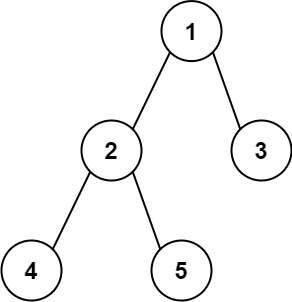
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 10<sup>4</sup>].
-100 <= Node.val <= 100

Answer

To solve this problem, we'll use a bottom-up approach to find the longest path in the binary tree. Here's the process:

For each node, calculate the longest path in its left and right subtrees.
The diameter at each node can be calculated by adding the lengths of the longest paths from the left and right children, plus two for the current node.
Keep track of the maximum diameter found during the traversal.
The final result will be the maximum diameter found across all nodes.

Height Calculation: For an empty node, return -1. For non-empty nodes, return 1 + max(left, right) where left and right are the heights of the left and right subtrees respectively.
Diameter Calculation: At each node, the longest path that passes through the node is 2 + left + right where left and right are the heights of the left and right subtrees. This term correctly counts the number of edges.

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.ans = 0

    def diameterOfBinaryTree(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def dfs(root):
            if not root:
                return -1
            left = dfs(root.left)
            right = dfs(root.right)
            self.ans = max(self.ans, 2 + left + right)
            return 1 + max(left, right)

        dfs(root)
        return self.ans

Let's go through an example together

Given this example
Let's go through the example root = [1, 2, 3, 4, 5] step-by-step using the provided code:Step-by-Step Execution

Initialization:
- A Solution object is created, initializing self.ans to 0.
Function Call:
- diameterOfBinaryTree(root) is called with the root of the tree (node with value 1).
DFS Function (Depth-First Search):
- dfs(root) is called with the root node (1).

Node 1 (Root)

DFS Call: dfs(1)
Left Subtree:
- DFS Call: dfs(2)

Node 2

DFS Call: dfs(2)
Left Subtree:
- DFS Call: dfs(4)

Node 4

DFS Call: dfs(4)
Left Subtree: dfs(None) returns -1 (no left child)
Right Subtree: dfs(None) returns -1 (no right child)
Calculate: left = -1, right = -1
Update Diameter: self.ans = max(0, 2 + (-1) + (-1)) = max(0, 0) = 0
Return Height: 1 + max(-1, -1) = 0
DFS Return: dfs(4) returns 0
Right Subtree:
- DFS Call: dfs(5)

Node 5

DFS Call: dfs(5)
Left Subtree: dfs(None) returns -1 (no left child)
Right Subtree: dfs(None) returns -1 (no right child)
Calculate: left = -1, right = -1
Update Diameter: self.ans = max(0, 2 + (-1) + (-1)) = max(0, 0) = 0
Return Height: 1 + max(-1, -1) = 0
DFS Return: dfs(5) returns 0
Calculate: left = 0, right = 0
Update Diameter: self.ans = max(0, 2 + 0 + 0) = max(0, 2) = 2
Return Height: 1 + max(0, 0) = 1
DFS Return: dfs(2) returns 1
Right Subtree:
- DFS Call: dfs(3)

Node 3

DFS Call: dfs(3)
Left Subtree: dfs(None) returns -1 (no left child)
Right Subtree: dfs(None) returns -1 (no right child)
Calculate: left = -1, right = -1
Update Diameter: self.ans = max(2, 2 + (-1) + (-1)) = max(2, 0) = 2
Return Height: 1 + max(-1, -1) = 0
DFS Return: dfs(3) returns 0
Calculate: left = 1, right = 0
Update Diameter: self.ans = max(2, 2 + 1 + 0) = max(2, 3) = 3
Return Height: 1 + max(1, 0) = 2
DFS Return: dfs(1) returns 2

Final Result:
- The final value of self.ans is 3, representing the longest path in the binary tree, which corresponds to the path [4, 2, 1, 3] or [5, 2, 1, 3]. Each path includes three edges, and hence the diameter is 3.

Thus, the function diameterOfBinaryTree(root) returns 3.

Time Complexity
The time complexity of this code is O(N) since we are visiting each node ounce and the operation of each node is O(N). Hence O(N) * O(1) = O(N)

Space Complexity
Space Complexity depends on the tree. If the tree is balanced then the recursion space complexity is O(log N) but if the tree is not balanced then in the worst case the space complexity is O(N).