Algo

Lowest Common Ancestor of a Binary Search Treen (Leetcode #235)

Nawat Sunthornyanakit's photo
Nawat Sunthornyanakit
·

3 min read

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

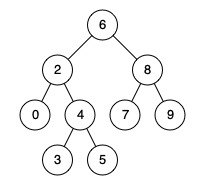
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [2, 10<sup>5</sup>].

  • -10<sup>9</sup> <= Node.val <= 10<sup>9</sup>

  • All Node.val are unique.

  • p != q

  • p and q will exist in the BST.

Answer

Explanation:

The problem of finding the lowest common ancestor (LCA) in a binary search tree can be simplified by leveraging the properties of BSTs:

  1. Binary Search Tree Property: In a BST, for any given node, all values in the left subtree are less than the node's value, and all values in the right subtree are greater than the node's value.

  2. Simplified Problem: Given two nodes p and q, we need to find the lowest common ancestor of these nodes. In other words, the LCA is the deepest node that is an ancestor of both p and q.

Approach:

  1. Recursive Traversal:

    • Start at the root of the tree.

    • If both p and q are less than the root's value, then both nodes must be in the left subtree. Recur on the left subtree.

    • If both p and q are greater than the root's value, then both nodes must be in the right subtree. Recur on the right subtree.

    • If p and q lie on different sides of the root (i.e., one is less than the root's value and the other is greater), then the root itself is the LCA.

Here is the updated code for finding the lowest common ancestor:

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        def dfs(root):

            # If both p and q are less than root, LCA must be in the left subtree
            if p.val < root.val and q.val < root.val:
                return dfs(root.left)

            # If both p and q are greater than root, LCA must be in the right subtree
            if p.val > root.val and q.val > root.val:
                return dfs(root.right)

             # This would be we have reach the terminate condition and we can return the answer
            return root

        return dfs(root)

Summary:

  • If p and q are both smaller than root, search in the left subtree.

  • If p and q are both larger than root, search in the right subtree.

  • If p and q lie on different sides of root, then root is the LCA.

This approach ensures that you efficiently find the LCA with minimal traversal.

Time Complexity:

  • Best Case (Balanced Tree): (O(\log N)), as the recursion depth corresponds to the height of the tree.

  • Worst Case (Unbalanced Tree): (O(N)), as the recursion depth in a highly unbalanced tree could be equal to the number of nodes.

Space Complexity:

  • Space Complexity: (O(H)), where (H) is the height of the tree. This is due to the space needed for the recursion stack. In a balanced tree, this would be (O(\log N)), while in an unbalanced tree, it could be (O(N)).
leetcodePython