Same Tree (Leetcode #100)

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

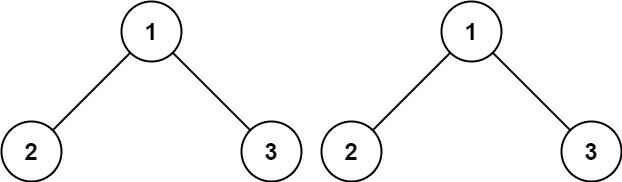
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

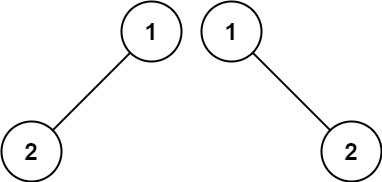
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

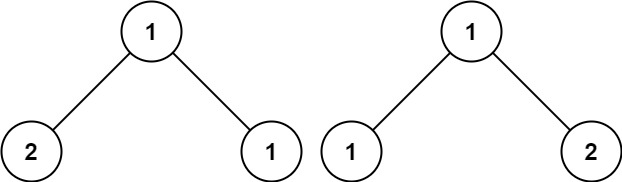
Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

• The number of nodes in both trees is in the range [0, 100].

• -10<sup>4</sup> <= Node.val <= 10<sup>4</sup>

Answer

This question is very simple. We have to check if every node in the same position has the same value. We can do this by using the DFS algorithm to visit every single node and check if they are the same.

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        def dfs(p,q):
            if not p and not q:
                return True
            if not p or not q:
                return False    
            if p.val != q.val:
                return False

            return dfs(p.left, q.left) and dfs(p.right, q.right)
        return dfs(p,q)

Let's go through this code step by step.

1. if not p and not q: If this is the case then we have reached the end of both trees and both are empty so in this case we will return True

2. if not p or not q: If this is the case then we have reached the end of one tree but not the other so the trees are not identical

3. if p.val != q.val: Finally, we check if the current values are the same.

4. return dfs(p.left, q.left) and dfs(p.right, q.right) will return True if all the True condition are met by all the nodes otherwise it will return False. This is because the and statement needs both conditions to be True to be True

Time complexity

Time complexity will be O(N) since we are visiting each node ounce and the operation is O(N)

Space Complexity

Since this is a DFS algorithm the space complexity will be O(N) in the worst case if the tree is unbalanced and O(logN) if the tree is balanced