Algo

Subtree of Another Tree (Leetcode #572)

Nawat Sunthornyanakit's photo
Nawat Sunthornyanakit
·

3 min read

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

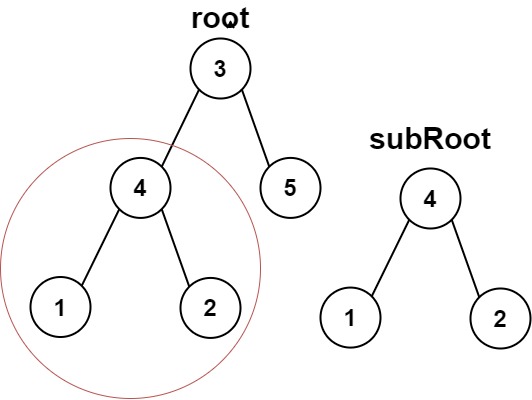
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

Example 2:

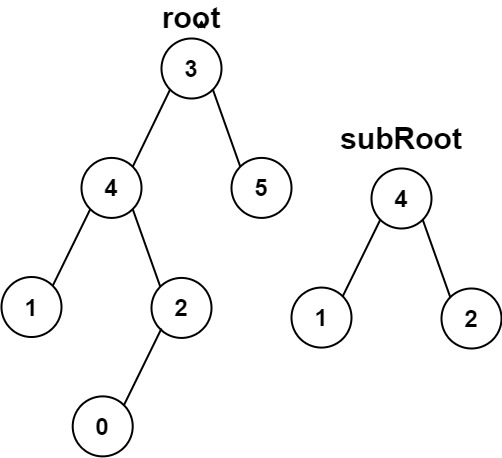
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

Constraints:

  • The number of nodes in the root tree is in the range [1, 2000].

  • The number of nodes in the subRoot tree is in the range [1, 1000].

  • -10<sup>4</sup> <= root.val <= 10<sup>4</sup>

  • -10<sup>4</sup> <= subRoot.val <= 10<sup>4</sup>

Answer

Before solving this question I recommend that you solve the Same Tree question first since we will be using algorithms from that question to solve this question. The simplest way to solve this question is to go through everything in the root until the root of the root and the root of the subRoot match then we can check if they are the same tree.

nary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def isSubtree(self, root, subRoot):
        """
        :type root: TreeNode
        :type subRoot: TreeNode
        :rtype: bool
        """
        def sametree(p,q):
            if not p and not q:
                return True
            if not p or not q:
                return False
            if p.val != q.val:
                return False
            return sametree(p.left,q.left) and sametree(p.right,q.right)
        def dfs(root,subRoot):
            if not root:
                return False
            if sametree(root,subRoot):
                return True    
            return dfs(root.right, subRoot) or dfs(root.left, subRoot)

        return dfs(root,subRoot)

I will not be focusing on the sametree function since I've already written about it in my other article. The dfs function can be broken down into the following steps.

  1. if we have reached the end of the tree we will return False since the subRoot is None

  2. if the current node leads to the same tree as the subTree we will return True since we have found a pair of tree

  3. Finally, since we are using or in the final return statement, we will return True if any node meets the same tree condition

Time Complexity

We need to break this down into two functions. The same tree function will have a time complexity of O(M) given there are m nodes in the subRoot. And since we are applying in the worst case the sameTree function on every node. Hence O(N) O(M) we will get the overall time complexity O(M * N)

Space Complexity

  1. sametree(p, q) Function:

    • The space complexity for the sametree function is determined by the depth of the recursion stack. In the worst case (for a completely unbalanced tree), this could be O(M) if subRoot has M nodes.

  2. dfs(root, subRoot) Function:

    • Similarly, the space complexity for the dfs function is determined by the depth of the recursion stack while traversing the root tree. In the worst case, this could be O(N) if root has N nodes.

Therefore, the overall space complexity is O(N + M) in the worst case due to the maximum depth of the recursion stack.

leetcodePython